In this paper, we porposed a statistical method for the estimation of the probability of invasion of fire blight disease via the importation of apple fruits, by considering that the proportion of infected fruits varies depending on the production area and the year. The following three assumptions, which might be applicable to biological invasions of several diseases of plants and animals, are used:

(1) A beta distribution approximately describes the probability distribution of the proportion of infected fruits in the production area of a given consignment,
(2) every consignment contains fruits that were drawn at random from the infinite population of the production area, and
(3) each infected fruit causes infection of fire blight in the importing country by an independent constant probability.

The estimate of the expected time required for invasion is 1707 years if we ignore the variability of infection, whereas the estimate is 334 years if we consider the variability. Thus, it is suggested that the estimation of the risk of invasion might be quite biased if we ignore the variability of infection.(Copyright by the Kluwer Academic Publishers)

Let us denote that
k : number of consignments imported during a year
n_i : number of fruits in the i th consignment
X_i : proportion of infected fruits in the production area of the i th consignment
Z_i : number of fruits causing fire blight in the importing country through the i th consignment
p : probability that an infected fruit causes the infection of fire blight in the importing country when it passed the port

The probability distribution of X_i is given by

........................................................(1)

The probability that at least one fruit causes infection in Japan is

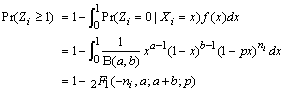......................................(2)

where ₂F₁ indicates the Gauss hypergeometric function. If we assume that the proportion of infection is constant irrespective of production area and year, the above probability is given by

......................................................................................(3)

The expected time required for invasion is approximately given by

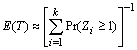........................................................................................(4)

In the case of fire blight disease, we obtain E (T) = 334 years by substituting Eq. (2) for Eq. (4). If we ignore the variability of the proportion of infection, we obtain E (T) = 1707 years by substituting Eq. (3) for Eq. (4). (Copyright by Kluwer Academic Publishers)