We develop a mechanistic model for pollen dispersal by a generalization of the Brownian motion model. This model provides an explanation as to why the probability distribution of the dispersal distance is leptokurtic in most organisms. The pollen is assumed to move in a period between t and t + Dt to the circumference of a circle of radius Dr_t that has a center at the current position. The angle of movement is chosen at random. Unlike the conventional Brownian motion model, the step length, Dr_t, fluctuates in a stochastic manner, obeying a generalized gamma distribution. The convection flow, i.e., the directional movement of pollen, is also considered. It is shown that this model is identical to the diffusion model where the dispersal duration weighted by the diffusion coefficient obeys a gamma distribution. Hence, the model is called the gamma model. The solution is given in an explicit form. The model is fitted to the 6 data sets obtained from the literature by maximizing the quasi-likelihood. Another model (the inverse gamma model), which is not a mechanistic model but a phenomenological model, is also fitted to the data to evaluate the validity of the gamma model.




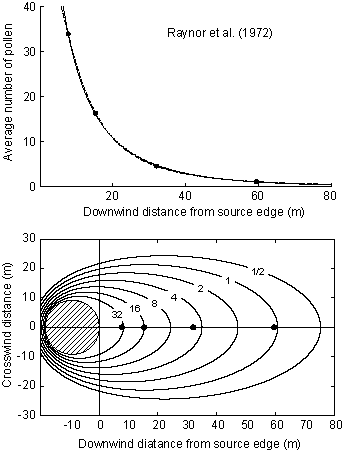
Figure 1.  Estimated curves for the data of Raynor et al. (1972; Agron J 64:420-427). Upper panel: Comparison between two models. The solid curve indicates the gamma model. The dotted curve indicates the inverse gamma model. Black dots indicate the observed average number of pollen grains captured by slides per 1 cm2 per day. The quantity is given by the percentage relative to the number of pollen grains captured at 1 m distance. Only the data used in the estimation of parameters are shown. Lower panel: Estimated contours of the average number of pollen grains. Black dots indicate the position of pollen samplers that were used in the estimation of parameters. The hatched circle indicates the pollen source. (Copyright by the Society of Population Ecology and Springer-Verlag Tokyo).