Difficulty in the prediction of expansion speed

Biological invasions are recurrent phenomena that cause global biotic changes, Prediction of the speed of range expansion is an important subject in controlling biological invasions. The speed of this expansion has been recorded for several species. However, we cannot always use the observed speed in one area as a way to predict the future speed of expansion in another area, because the speed may differ strongly depending on the destination’s environment. Observed speed will be limited by various factors such as the spatial rareness of food plants, unfavorable temperature for reproduction, and the existence of natural enemies. When a species is accidentally introduced into a highly suitable environment, it may expand its distribution range at a high speed never before observed. It is thus necessary to theoretically predict the potential expansion speed in managing invading species.

Gamma model and Einstein’s model

Estimation of the probability density function (PDF) of dispersal distance, called the dispersal kernel, is of first importance in estimating the potential speed of range expansion. Empirical analysis of an organism‘s movement has indicated that the actual dispersal kernel is more leptokurtic than the Gaussian distributions which were derived by a Brownian motion model; the tail of the distribution is fatter than that of the normal distribution.

Bachelier (1900) is known to be the first person who formulated the Brownian motion model in the field of economics (Mantegna and Stanley 1999). In the field of physics, Einstein (1905) first derived Gaussian distributions in the Brownian motion model from more flexible assumptions. He assumed that the particles move randomly in any direction instantaneously and that the step length of movement fluctuates obeying a distribution. Although he allowed the fluctuation of step length, he did not consider the temporal fluctuation of the distribution of step length. In contrast to Einstein’s approach, Yamamura (2004) assumed that the step length does not vary at a given time and that the step length fluctuates temporally. Then, he derived a model called the gamma model. When an individual begins its dispersal from the origin (0, 0) at a time t = 0, the probability density that the individual is at (x, y) after a time is given by

-------------------------------(1)

We applied the gamma model to estimate the potential speed at which the ragweed beetle, Ophraella communa LeSage, which was accidentally introduced into Japan, expands their range of distribution. Figure 1 shows fitted curves for the gamma model and Brownian motion model.

 

Figure 1. Estimated dispersal kernel of the gamma model. Dispersal kernel of Brownian motion model is also shown for comparison. Each circle indicates the observed number of individuals that were captured by a yellow sticky trap placed at that distance. Solid curve indicates the gamma model. Dotted curve indicates the Brownian motion model that was estimated by the maximum quasi-likelihood method.

Potential speed of range expansion

In the gamma model we can predict the asymptotic speed of range expansion (c) per generation by the following equation.

---------------------(2)

where R 0 is the potential number of adult individuals that are yielded per adult. l is a parameter of the gamma model. For the ragweed beetle, we have R 0 = 323.7 and l = exo(-19.1). Then, the speed of expansion per generation is predicted to be 82.2 km. The beetle reprocude 4 generations in Ibaraki prefecture. Then, we can predict the expansion speed per year by replacing R 0 in Eq. 2 by R 0^4. The estimated speed per year is 328.6 km.

Realized speed of range expansion

The realized speed of expansion should be smaller thant the potential speed, becasue several mortality arise in the fields. We estimated the actual expansion speed by approximating the distribution range of the beetle by a half circle whose center is placed at the port of introduction. The estimates are shown in Fig. 2.

 

Figure 2. Observed speed of range expansion of O. communa. The distance from the port of introduction was estimated by assuming that the distribution range can be approximately expressed by a half circle.

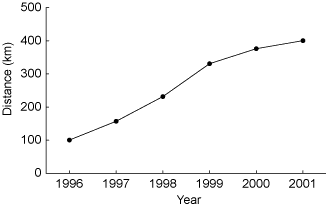
The observed speed decelerated after 1999. The least squares estimate of speed between 1996 and 1999 was 76.5 km per year. Thus, the realized speed of expansion is considerably smaller than the potential speed (328.6 km per year) which could be attained in an optimal environment.

References

Bachelier L (1900) Theorie de la speculation. Annales Scientifiques de l'Ecole Normale Superieure Ser (III) 17:21--86 [PDF 7,979KB]
Einstein A (1905) On the movement of small particles suspended in a stationary liquid demanded by the molecular-kinetic theory of heat (English translation, 1956). In: Furth R (ed) Investigations on the theory of the Brownian movement. Dover, New York, pp 1--18
Moriya S, Tanaka K, Yamamura K, Shimizu T, Shiyake S (2002) Expansion of the distribution range of the ragweed beetle, Ophraella communa LeSage, (Coleoptera: Chrysomelidae) and its natural enemies in Japan (in Japanese with English summary). Ann Rept Kanto-Tosan Plant Prot Soc 49:131-133.
Yamamura K (2004) Dispersal distance of corn pollen under fluctuating diffusion coefficient. Popul Ecol 46:87--101 [PDF (577KB)]