Random median sampling

Recommending the arbitrary sampling

When we examine the number of insects per plant in fields, the labor becomes large if we encounter a plant that contains many insects unluckily. We consume a large amount of labor in counting the total number of insects on the selected plant. In this case, we feel an urge to change the plant to another plant that contains a fewer number of insects. However, such an arbitrary change of plants is not permitted. We must, in principle, select the plant at random to count the number of insects. Otherwise, the estimates will be biased.

However, under some conditions, we can change the selected plant arbitrarily when the plant contains too many insects. The random median sampling of Wada et al. (2007) is a sampling procedure that enables such an arbitrary selection of samples.

Random median sampling

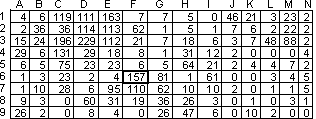
In performing random median sampling, we first select a sampling item at random from the sampling area. We roughly compare the abundance of individuals in the selected item with that of the adjacent two items in order to identify the item that has median abundance, i.e., the item that has the second largest abundance among the three items. We count the number of individuals of the item having the median abundance. This procedure is repeated n times in the sampling area (i = 1, 2, …, n). Let mi be the ith median abundance. The estimates of the mean abundance per sampling item and the variance of estimates are given by S mi/n and S(mi - Smi/n)^2/n(n - 1), respectively. Figure 1 indicates an illustrative example.

ミカンハダニの空間分布

Fig. 1. Illustrative example of random median sampling. The spatial distribution of the number of citrus red mites per tree (75 leaves) is shown. When we selected the tree at the 6F position (indicated by a bold square) by random sampling, for example, we only counted the number of mites on the tree at the 6G position that had the median abundance among the adjacent three trees at the 6E, 6F, and 6G positions. (Redrawn from Shizuoka Prefectural Citrus Experiment Station, 1970)

Effectiveness of random median sampling

Random median sampling is effective when the correlation coefficient between adjacent items is small. If the correlation coefficient is close to zero, random median sampling reduces the variance of estimates to 45% or 32% of that in simple random sampling when the distribution follows a normal distribution or a Laplace distribution, respectively (Fig. 2). The sample size required to achieve a given precision of estimate decreases accordingly. The effectiveness of random median sampling, however, is small if the correlation coefficient is large.

Reduction of variance by RMS

Fig. 2. Reduction in the variance of estimates within local subpopulations. The ratio of reduction in local variance, Vi(mi)/sw2, was calculated by numerical integration.

References

Shizuoka Prefectural Citrus Experiment Station (1970) Report of the survey in 1969 for the establishment of the forecasting method of citrus red mite (in Japanese). Shizuoka Prefectural Citrus Experiment Station.
Wada T, Urano S, Yamamura K (2007) A laborsaving sampling method to estimate a normal distributed population by a kind of two-stage sampling using a median. Appl Entomol Zool 42:9-14 [PDF 225KB, download from JSTAGE].