Yamamura K, Ishimoto M (2009) Optimal sample size for composite sampling with subsampling, when estimating proportion of pecky rice grains in a field. Journal of Agricultural, Biological, and Environmental Statistics 14:135-153. [Preprint PDF(562KB)] (Final version of manuscript) The original publication is available at http://www.amstat.org/publications/jabes.cfm

Problem in estiamtion

The proportion of pecky rice grains has been empirically estimated using composite sampling with subsampling. The procedure is summarized as follows: (1) a fixed number of rice plants (n₁) are drawn at random in the paddy field; (2) all the rice grains in the collected rice plants are mixed well to form a composite; (3) a portion of the grains (n₂) are drawn at random from the composite; and (4) the collected grains are examined by eye to estimate the proportion of pecky rice grains. We propose a method to determine the optimal sample size in estimating the proportion of defective items by this kind of composite sampling with subsampling.



Figure 1. Schematic illustration of the sampling scheme of estimating the proportion of pecky rice grains.

Model

We use the following notations.
s = the number of grains in the ith plant,
n₁ = the number of drawn rice plants,
n₂ = the number of rice grains drawn from the composite,
P_i = the probability that a rice grain around the ith plant is pecky,
P₀ = the average of P_i over the sampling field, i.e., P₀ = E(P_i)
c₁ = the cost that is required to collect one rice plant,
c₂= the cost that is required to examine one rice grain.
The expectation and the variance of the estimated proportion of P₀ is given by




We regulate the precision of estimates by the relative precision that is defined by the coefficient of variation (CV),



The proportion of pecky rice grains varies depending on the position in the paddy field. We describe the spatial distribution of the proportion of pecky rice grains by a gamma distribution as an approximation. We describe the relation between the mean and variance by using Talyor's power law. Let μ and σ² be the spatial mean and variance of the number of insects, respectively. Taylor's power law is defined by,



Then, we can obtain the combination of n₁ and n₂ that achieves the relative precision D by

Example of calculation

We empirically consider that D = 0.25 is most appropriate as standard. We must estimate the costs (c₁ and c₂), to determine the optimal sample size. About 60 seconds are required in drawing a rice plant and in shelling the rice grains. About 0.12 seconds are required to examine a rice grain on average. We thus use c₁/c₂ = 60/0.12 = 500. The grade of rice falls from the first grade to the second grade if the proportion of pecky rice grains is larger than 0.001 Thus, we use P_c = 0.001. We estimated the parameters of Taylor's power law from field data. The combination of n₁ and n₂ is shown by Fig. 2. We obtained the optimal sample size n₁ = 58 and n₂ = 31000.



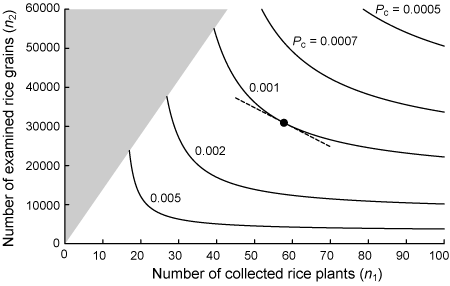
Figure 2. Sample size to achieve a given relative precision (D). The curves indicate the combination of n₁ and n₂ that achieve D < 0.25 for all P₀ in the range of P₀ > P_c. Five curves for different values of P_c are shown. The solid circle indicates the optimal combination of n₁ and n₂ for P_c = 0.001 and (c₁/c₂) = 500. The broken line indicates a slope of −500. The shaded area indicates the nonexistent combination of n₁ and n₂ where the required number of drawn grains exceeds the total number of drawn grains, i.e., the region ofn₂ > sn₁. The following parameters were used: s = 1400, a = exp(−2.19), and b = 1.60.