Identifying the environmental factors determining the abundance of organisms

Organisms are subjected to various mortality factors, each of which causes different mortality in each of life stages of the organism. The factor that contributes most to the population fluctuation should be called the 'key-factor'. Similarly, the stage that contributes most to the population fluctuation should be called the 'key-stage'. The conventional key-factor analyses divide the variation of K into the variation of ki, where K is the total mortality through all stages, and ki is the mortality in the i th stage. These analyses identify the key-stage, but do not identify the key-factor, unless each stage is subjected to only a single mortality factor. Hence, the conventional key-factor analyses should be called key-stage analyses. We propose a 'key-factor key-stage analysis' by integrating the conventional key-factor analyses and ANOVA, emphasizing the importance of discriminating between the key-factor and the key-stage. This analysis identifies the key-factor, the key-stage, and the combination of factor and stage that is most influential in determining the fluctuation of total mortality.

Please download the R funciton and SAS macro for performing key-factor/key-stage analysis



 Example analysis using JMP

(1) Analysis of abundance

Table 1.  Life table of the beet semi-looper Autographa nigrisigna to illustrate the usefulness of key-factor/key-stage analysis. s0 indicates the natural logarithm of the number of individuals of the 1st stage larvae. si (i = 1, 2, 3) indicate the natural logarithm of survival rate of the i th stage larvae. loge(N4) indicates the natural logarithm of the number of individuals of the 4th instar larvae.

Experiment number
Experimental block
Plant density
s0
s1
s2
s3
loge(N4)
1
1
sparse
3.0375
-0.6876
-0.5116
-0.8171
1.0212
2
2
sparse
3.1587
-1.0309
-0.7252
-0.8148
0.5878
3
3
sparse
3.2480
-0.9627
-0.6292
-0.6503
1.0059
4
4
sparse
2.9592
-0.6798
-0.6759
-1.2202
0.3833
5
1
dense
2.4684
-0.7314
-0.5615
-0.4142
0.7613
6
2
dense
2.3188
-0.8368
-0.3829
-0.6250
0.4741
7
3
dense
2.3946
-0.6550
-0.4126
-0.4743
0.8527
8
4
dense
2.8446
-0.8896
-0.5469
-0.2750
1.1330



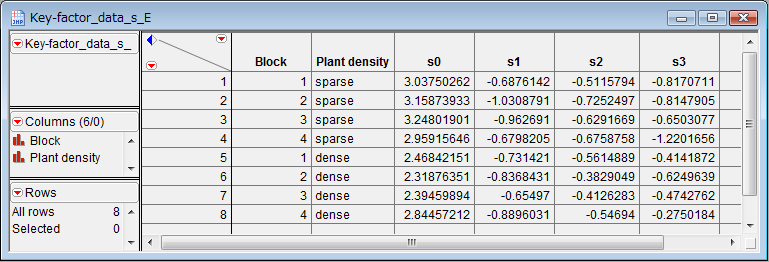
Original data showing the abundance of beet semi-looper (BSL)
Figure 1.   Data table for JMP.
Double click the column title 'Block' to modify the property of variable. Set 'Modelling type' nominal.


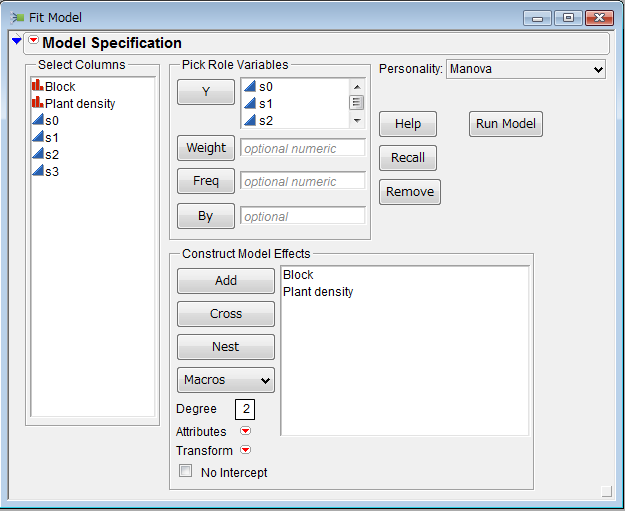
Model fitting dialog in JMP software
Figure 2.  The above dialog box appears when we select 'Fit Model' from 'Analyze' menu of the menu bar. Select s0, s1, s2, s3 from 'Select Columns' box and drag them into 'Y' box. Select 'Block' and 'Plant density' from 'Select Columns' box and drag them into 'Construct Model Effects' box. Select the 'Manova' from the 'Personality' pull down menu in the dialog box. Then, perform analysis by pushing 'Run Model' button.


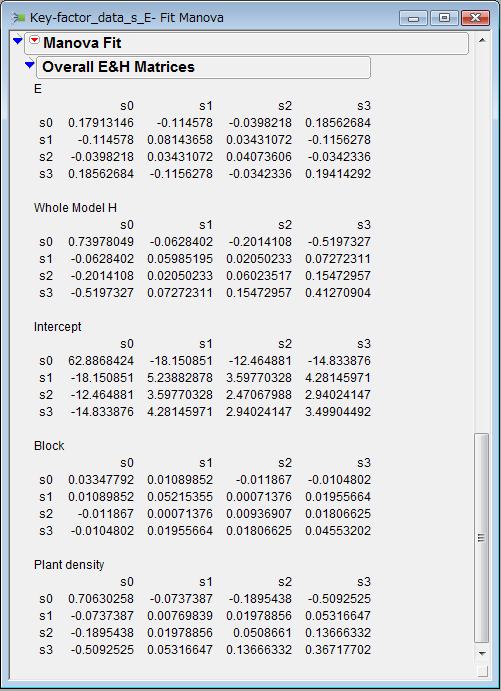
SSCPM for BSL
Figure 3.  Open the 'Overall E&H Matrices' in the result window. (This matrix is folded in the first view.) Add the s0 row of 'Block' matrix. Then, we obtain 0.03347792 + 0.01089852 + 0.011867 - 0.0104802 = 0.02202924. This quantity indicates the amount of contribution of 'Block' through the abundance in the first stage (s0). Add the s1 row of 'Block' matrix. Then, we obtain 0.01089852 + 0.05215355 + 0.00071376 + 0.01955664 = 0.08332247. This quantity indicates the amount of contribution of 'Block' through the survival rate in the first stage (s1). Perform the similar calculation for each row of the following three matrices: Block, Plant density, and E. Then, we obtain the key-factor/key-stage analysis table by arranging the calculated 12 quantities.


Table 2.   Key-factor/key-stage table. Components are multiplied by 10000 to facilitate the mutual comparison.
Factor
df
Stage
Total
s0
s1
s2
s3
Block
3
220.3
833.2
162.8
726.7
1943.1
Plant density
1
-662.3
69.1
177.7
477.5
62.1
Residual
3
2103.6
-1144.6
9.9
2299.1
3268.0
Total
7
1661.6
-242.2
350.5
3503.4
5273.2



Example analysis using JMP
(2) Analysis of mortality

Table 3.  Life table of the beet semi-looper Autographa nigrisigna to illustrate the usefulness of key-factor/key-stage analysis. ki (i = 1, 2, 3) indicate the negative natural logarithm of survival rate of the i th stage larvae.

Experiment number
Experimental block
Plant density
k1
k2
k3
K
1
1
sparse
0.2986
0.2222
0.3548
0.8757
2
2
sparse
0.4477
0.3150
0.3539
1.1165
3
3
sparse
0.4181
0.2732
0.2824
0.9738
4
4
sparse
0.2952
0.2935
0.5299
1.1187
5
1
dense
0.3177
0.2439
0.1799
0.7414
6
2
dense
0.3634
0.1663
0.2714
0.8011
7
3
dense
0.2844
0.1792
0.2060
0.6696
8
4
dense
0.3863
0.2375
0.1194
0.7433



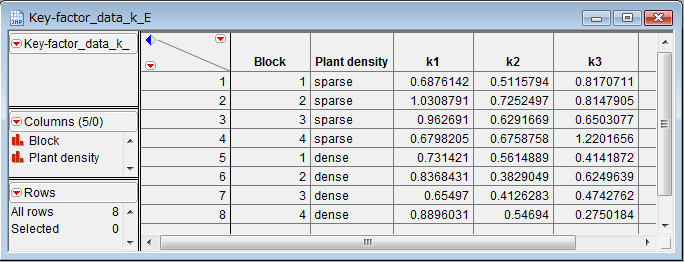
Original data showing the abundance of beet semi-looper (BSL)
Figure 4.   Data table for JMP.
Double click the column title 'Block' to modify the property of variable. Set 'Modelling type' nominal.


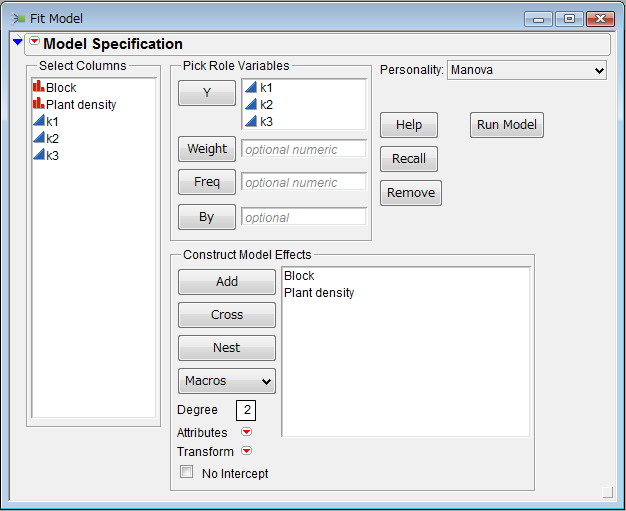
Model fitting dialog in JMP software
Figure 5.  The above dialog box appears when we select 'Fit Model' from 'Analyze' menu of the menu bar. Select k1, k2, k3 from 'Select Columns' box and drag them into 'Y' box. Select 'Block' and 'Plant density' from 'Select Columns' box and drag them into 'Construct Model Effects' box. Select the 'Manova' from the 'Personality' pull down menu in the dialog box. Then, perform analysis by pushing 'Run Model' button.


SSCPM for BSL
Figure 6.  Open the 'Overall E&H Matrices' in the result window. (This matrix is folded in the first view.) Add the k1 row of 'Block' matrix. Then, we obtain 0.05215355 + 0.00071376 + 0.01955664 = 0.07242395 . This quantity indicates the amount of contribution of 'Block' through the survival rate in the first stage (k1). Perform the similar calculation for each row of the following three matrices: Block, Plant density, and E. Then, we obtain the key-factor/key-stage analysis table by arranging the calculated 9 quantities.


Table 4.   Key-factor/key-stage table. Components are multiplied by 10000 to facilitate the mutual comparison.
Factor
df
Stage
Total
k1
k2
k3
Block
3
724.2
281.5
831.5
1837.3
Plant density
1
806.5
2073.2
5570.1
8449.8
Residual
3
1.2
408.1
442.8
852.1
Total
7
1532.0
2762.8
6844.4
11139.2



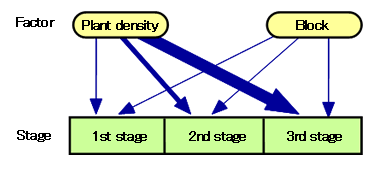
Graphical presentation of the result from key-factor/key-stage analysis

Figure 7.   Illustration of the result of key-factor/key-stage analysis . Thickness of arrows is proportional to the corresponding component in Table 2. The arrow that connects the plant density and 3rd stage larvae is extremely thick. Therefore, it is indicated that the number of the 4th stage larvae is principally determined by the plant density through the survival rate of the 3rd stage larvae.





Return to list of topics